SPIN VERIFICATION EXAMPLES AND EXERCISES
Included below are some verification exercises that can help you get acquainted with the Spin model checker. All examples used here are available as Promela files in the Examples directory of the Spin distribution.0. Installing Spin
We will assume you are using the most recent version of Spin, which at the time of writing is Version 6.4.8. If Spin is not yet installed on your machine, do this (assuming a linux-like machine):$ cd $ wget http://spinroot.com/spin/Src/spin648.tar.gz $ tar -xzvf spin648.tar.gz $ cd Spin/Src6.4.8 $ make $ cp spin /usr/local/bin # on a Mac: cp spin /usr/bin $ cd ../Examples/Exercises $ spin -V # make sure it's there Spin Version 6.4.8 -- 19 January 2018
1. Evaluating Search Complexity
This first set of exercises is meant to give an indication of the nature of the state space explosion phenomenon, and how Spin deals with it. It consists of a set of small problems that can be solved with Spin. At each step, first try to determine what should happen, write down your prediction, and only then perform the experiment with Spin, and explain the result if it differs from what you thought would happen.Answer each of the questions marked a) ... k), spending as much time as you need to understand what really happens.
a) How many reachable states do you predict will the following small ProMeLa model generate?
init { // file: ex_1a.pml
byte i // initialized to 0 by default
do // loop forever
:: i++ // short for i = i + 1
od
}
Try a simulation run of 514 steps:
$ spin -u514 -p -l ex_1a.pml # print out local vars at every stepNotice what happens with the value of byte variable i on the 255-th increment (in step 511).
You can see all options that Spin supports by executing:
$ spin --i.e., using two dashes as the argument.
b) Would the simulation terminate if you didn't limit the number of steps?
c) The model allows for an infinite number of increments of variable i. Is this still a finite state model?
$ spin -run -dump ex_1a.pmlor just
$ spin -run -d ex_1a.pml
$ spin -run ex_1a.pmlExplain the output and the number of states that is reported.
$ spin -a ex_1a.pml # generate a C verifier for the model in pan.c $ cc -o pan pan.c # compile it $ ./pan # execute itSpin's -run argument separates arguments processed by Spin in interpreting the model itself (these would go before the -run argument) and arguments that are used to compile and run the verifier (these would go after the -run argument). In our example we needed no additional arguments of either type.
e) What would happen if you had declared the variable to be of type short instead of byte ? What if you use a bit ? Try these with a verification run and explain the results.
f) Predict how many reachable states there are for the following system, and write them down as a reachability tree.
#ifndef N
#define N 2
#endif
init { // file: ex_1f.pml
chan dummy = [N] of { byte } // a message channel of N slots
do
:: dummy!85 // send value 85 to the channel
:: dummy!170 // send value 170 to the channel
od
}
$ spin -DN=4 -m -run ex_1f.pml
$ spin -m -run ex_1f.pml # use -m to ignore buffer overflowExplain the result.
An invalid endstate does not always correspond to an actual deadlock. If it does not, we can label the state where a process is okay to stop with an end-state label. We can place one at the first do keyword in the model, for instance, and then you'd be free to omit the -m flag, since the verifier now knows that it is okay to block the init process at that point in the code. You should get the same number of reachable states as before:
init {
chan dummy = [N] of { byte } // a message channel of N slots
end: do
:: dummy!85 // send value 85 to the channel
:: dummy!170 // send value 170 to the channel
od
}
g) What happens if you set N to 3, 4, 5, etc. ? Express the number of states as a function of N. Use your formula to calculate how many states there will be if you set N to 14 ? Check your prediction as follows.
$ spin -DN=14 -m -run ex_1f.pmlSet N to 20 and repeat the run.
$ spin -DN=20 -m -run ex_1f.pml
Consider the following metrics on this verification run:
T: the elapsed time for the run that is reported at the end S: the number of states stored G: the number of total number of states stored and matched V: the State-vector size (the amount of memory needed to store one state)
T measures only the time needed to perform the verification. It excludes the time needed for the generation and compilation of the verification code itself. (At higher settings for compiler optimization, and for more complexi models, this can introduce a notable time delay as well.)
G counts not just new states visited in the search, but also states that were re-visited (matched), so it reflects more accurately how much work was done by the verifier.
S/T (or G/T) gives you a measure for the efficiency of the verification process, or the rate at which reachable states are processed. Generally this rate will depend on a number of factors, including the size S, and, of course, the speed of your machine. For Spin this rate is typically in the range 105 to 106 states per second. We look at a few other factors that can influence performance below.
S*V gives you the amount of memory that would be needed to store the full state space without compression. The statespace is not the only place where memory is used during the search (e.g., the stack also consumes memory) but it is typically the largest factor.
h) The efficiency of a reachability analysis also depends critically on the state space storage algorithm that is used. By default, Spin uses a standard hash-table with linked lists to store states. To study the effect of the hash-table size on performance, repeat the last verification run with a very small hash table, for instance as follows:
$ spin -DN=20 -m -run -w12 ex_1f.pml
Try different settings for the -w argument. Notice that the number of states stored does not change, but the number of hash-conflicts, and the runtime needed, does.
i) How much memory would you need to do a verification run for our last example with N=24 ?
16 MB is 224 bytes, so we could store no more than 16,777,216 / 42 = 399,457, or about 399,000 reachable states in this much memory. Other parts of the verification consume some memory as well, so this is an upper-bound only. To find out the real number, try it as follows. In this command we limit the search to 16 MB plus a 1 MB margin, and we use a small hashtable size (-w15:
$ spin -DN=24 -m -run -DMEMLIM=17 -w15 ex_1f.pml
All arguments that follow a -run argument are passed by Spin to either the compiler or the runtime verifier. In this case we used both types of pass-thru options. All arguments that preceed the -run argument are processed by Spin itself as before.
If the real statespace size is2(N+1)-1 states (33,554,431), what fraction of that statespace did you cover in your verification run? Is it more than 1%?
j)
Let's see if we can improve over that last result,
without increasing the amount of memory.
Perform a bitstate search with Spin, as follows.
$ spin -DN=24 -m -run -DMEMLIM=17 -bitstate ex_1f.pmlThe default argument for -w gives us precisely the right size of the hash-array of 16 MB here. (The default is -w27). Compare the number of states stored with that of the earlier run. It should have increased to about 64% of the actual number that you calculated before: a significant increase.
We can improve our chances of finding errors even more if we repeat the run with different hash-functions. By changing hash-functions we can achieve that hash-conflicts (which now remain unresolved and lead to truncation of the search) appear in different places, meaning that a different sampling of the state space will result. Spin has 100 different hash-functions builtin. You can change the default of -h1 to for instance -h71 to get a different sampling of the statespace.
One other things you can vary, to influence the sampling, is the number of bits that is set per state (i.e., the number of independent hash-functions that is used per state). You do so by specifying a -k argument. The default is -k3, which sets three bit-positions per state by using three independent hash-functions, but you can specify any other value greater than zero.
k)
The default setting for the -w argument in a bitstate search
is -w27. This defines a bitstate hash-array size of 227
bits, which at 8 bits per byte equals 224 bytes, or 16 MB.
In a bitstate search the -w argument does determine the
maximum number of states that can be recorded in the bitstate hash-array.
Repeat the run without the memory bound, and enable
some compiler optimization while you're at it, as follows:
$ spin -DN=24 -m -run -O2 -bitstate -w29 ex_1f.pmland perform some additional runs with different sizes of the bitstate array (different from the default of -w27). Notice how the coverage achieved is changing for smaller and larger hash-array sizes.
For added credit, check also how the performance changes if you compile with or without different levels of compiler optimization, e.g., -O, -O2, or -O3.
2. Verifying a Protocol
The figure below shows a protocol specification given by Bartlett et al. This figure appears as Figure 3c in the paper referenced, which introduced what became known as the alternating-bit protocol. It was originally designed to make it possible to transmit information reliably over noisy telephone lines with low-speed (e.g., 300 baud) modems.
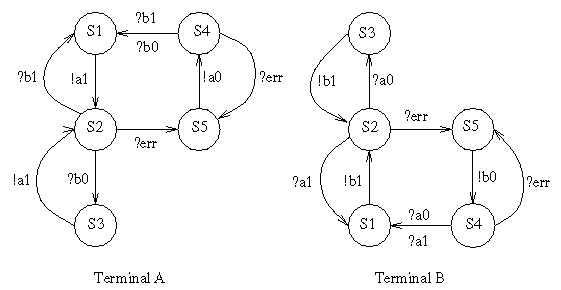
A (partial) Promela version of this protocol is shown below.
State S1 is the initial state in process A and state S2 is the initial state in process B.
1 mtype = { a0, a1, b0, b1, err } // file ex_2.pml
2
3 chan a2b = [0] of { mtype } // a rendezvous channel for messages from A to B
4 chan b2a = [0] of { mtype } // a second channel for the reverse direction
5
6 active proctype A()
7 {
8 S1: a2b!a1
9 S2: if
10 :: b2a?b1 -> goto S1
11 :: b2a?b0 -> goto S3
12 :: b2a?err -> goto S5
13 fi
14 S3: a2b!a1 -> goto S2
15 S4: b2a?err -> goto S5
16 S5: a2b!a0 -> goto S4
17 }
18
19 active proctype B()
20 {
21 goto S2
22 S1: b2a!b1
23 S2: if
24 :: a2b?a0 -> goto S3
25 :: a2b?a1 -> goto S1
26 :: a2b?err -> goto S5
27 fi
28 S3: b2a!b0 -> goto S2
29 S4: a2b?_ -> goto S1
30 S5: b2a!b0 -> goto S4
31 }
a)
Use a spin verification to see if there are any unreachable states.
Explain the result.
b) How would you modify the model to make all states reachable?
Like this:
S1: if :: b2a!b1 // correct transmission :: b2a!err // model message corruption fi
-
"Every message fetched by A is received error-free
at least once and accepted at most once by B."
chan a2b = [0] of { mtype, byte }
chan b2a = [0] of { mtype, byte }
where the send and receive operations now have two field of
matching types. For instance:
a2b!a1(78)You can find more hints about proving this type of property in the last problem in this set, below.
3. Verifying a Mutual Exclusion Algorithm
If two or more concurrent processes execute the same code and access the same data, there is a potential problem that they may overwrite each others results and corrupt the data. The mutual exclusion problem is the problem of restricting access to a critical section in the code to a single process at a time, assuming only the indivisibility of read and write instructions. The problem was first described by Edsger Dijkstra.
It is especially important to note that mutual exclusion algorithms that do not use any special machine instructions no longer work correctly on modern CPU architectures with out-of-order execution. On these machines (i.e., the machine your using now, no matter which brand it is) the problem can not be solved under the constraints that Dijkstra defined in 1965. Nonetheless, for mysterious reasons, mutual exclusion algorithms still remain popular as examples of the application of logic model checking.
a) Dijkstra published a first solution to the problem (that worked on the CPUs from that time) in his 1965 paper. A year later a different author published an "improved" solution" in the same journal (Comm. of the ACM, Vol. 9, No. 1, p. 45). It is reproduced here as it was published (in pseudo Algol).
1 Boolean array b(0;1) integer k, i, j, 2 comment process i, with i either 0 or 1 and j = 1-i; 3 C0: b(i) := false; 4 C1: if k != i then begin 5 C2: if not (b(j) then go to C2; 6 else k := i; go to C1 end; 7 else critical section; 8 b(i) := true; 9 remainder of program; 10 go to C0; 11 endModel this algorithm as a Spin model, and prove or disprove the correctness of the algorithm. You do not need to, and should not, consider out of order executions.
$ spin -run ex_3a.pml $ spin -p -replay ex_3a.pmlIn this sample solution an LTL property is used to verify the algorithm. You can also verify this simple safety property with a plain assertion. For hints on how to do that, see the suggestion box at problem 3b below. For more suggestions for replaying counter-examples, or finding shorter alternative sequences, look for the suggestion box under problem 3c below.
b) The mutual exclusion problem was popular as an intellectual challenge for a very long time. For an overview solution attempts up to roughly 1984, see Raynal or Lamport. An elegant solution was published by Peterson. In Promela the solution can be modeled as follows. The predefined Promela variable _pid contains the id of the running process: which in this case is either 0 or 1.
1 bool flag[2] // file: ex_3b.pml
2 bool turn
3
4 active [2] proctype user()
5 {
6 flag[_pid] = true
7 turn = _pid
8 (flag[1-_pid] == false || turn == 1-_pid)
9
10 crit: skip // critical section
11
12 flag[_pid] = false
13 }
Verify Peterson's algorithm with Spin.
9 cnt++ 10 crit: assert(cnt == 1) 11 cnt--Additional questions: what data type should cnt have? Could it be a bit? Could it be an int? Should it? Could the variable cnt be declared locally instead of globally? Explain your answer.
c) Far too many publications contained what later turned out to be faulty solutions to the mutual exclusion problem. In the sixties and seventies there were no model checkers to quickly find out whether or not a solution was sound. As an example, the next version of the algorithm was recommended by a computer manufacturer to a customer in the late eighties.
1 byte cnt // file ex_3c.pml
2 byte x, y, z
3
4 active [2] proctype user()
5 { byte me = _pid+1 // 1 or 2
6
7 L1: x = me
8 if
9 :: (y != 0 && y != me) -> goto L1 // try again
10 :: (y == 0 || y == me)
11 fi
12 z = me
13 if
14 :: (x != me) -> goto L1 // try again
15 :: (x == me)
16 fi
17 y = me
18 if
19 :: (z != me) -> goto L1 // try again
20 :: (z == me)
21 fi // success
22 cnt++
23 assert(cnt == 1) // critical section
24 cnt--
25 goto L1 // Dijkstra wouldn't like this either
26 }
First try to find a scenario that leads to the assertion
violation by studying the algorithm.
Next generate the counter-example with Spin.
$ spin -replay ex_3c.pmlwhich will show you a final value for the global variable cnt of 2, but it doesn't show the steps leading to the assertion violation. To do so you will have to add some more options, telling Spin what to print at each step. For instance:
$ spin -p -replay ex_3c.pmlis far more informative.
You'll also notice that the trail is longer than it would need to be. To get a shorter trail, you can try running the verification with an iterative shortening option -i. For instance
$ spin -run -i ex_3c.pml # add runtime parameter -i $ spin -p -replay ex_3c.pml# -p goes before -replay This is still not the shortest possible trail. To get that, you can recompile Spin to force it to search for the shortest possible counter-example. For instance by using a breadth-first, instead of the default depth-first search, as follows:
$ spin -run -bfs ex_3c.pml # use breadth-first search $ spin -p -replay ex_3c.pmlYou can also get the shortest counter-example with the default depth-first search, but now you have to tell the verifier to remember the length of execution sequences (which uses more memory) and use the iterative shortening method:
$ spin -run -i ex_3c.pml # modified depth-first with shortening $ spin -p -replay ex_3c.pml
4. Verifying Petri Nets
It is often easier to build a small Spin model and ask the model checker to verify it than it is to write or to check a thorough manual proof of correctness. Petri Nets are relatively easy to model as Promela verification models. For this exercise, consider the Petri Net model shown below, which first appeared as Figure 1 in Berthelot et al.
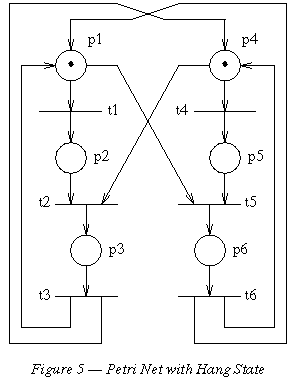
A Spin model for this Petri net can be written as follows.
1 #define Place byte // assume at most 255 tokens per place
2 // file ex_4.pml
3 Place p1=1, p2, p3 // place p1 has an initial token
4 Place p4=1, p5, p6 // place p4 has an initial token
5
6 #define inp1(x) x>0 -> x--
7 #define inp2(x,y) x>0 && y>0 -> x--; y--
8 #define out1(x) x++
9 #define out2(x,y) x++; y++
10
11 init
12 {
13 do
14 :: inp1(p1) -> out1(p2) // t1
15 :: inp2(p2,p4) -> out1(p3) // t2
16 :: inp1(p3) -> out2(p1,p4) // t3
17 :: inp1(p4) -> out1(p5) // t4
18 :: inp2(p1,p5) -> out1(p6) // t5
19 :: inp1(p6) -> out2(p4,p1) // t6
20 od
21 }
The net was proven to be deadlock free in the paper referenced, with a manual reduction and proof technique. Verify the result with Spin. Explain the result in detail.
5. Veryfying a Process Scheduling Algorithm
The model below for implementing sleep and wakeup routines in a distributed operating systems kernel is based on Ruane's description. The model contains an error that can be detected as a fair non-progress cycle (use runtime options -l and -f). Check if the proposed fix by Ruane, indicated in the model, suffices to remove the problem.
1 mtype = { Wakeme, Running } // file ex_5.pml
2
3 bit lk, sleep_q
4 bit r_lock, r_want
5 mtype State = Running
6
7 active proctype client()
8 {
9 sleep: // sleep routine
10 atomic { (lk == 0) -> lk = 1 } // spinlock(&lk)
11 do // while r->lock
12 :: (r_lock == 1) -> // r->lock == 1
13 r_want = 1
14 State = Wakeme
15 lk = 0 // freelock(&lk)
16 (State == Running) // wait for wakeup
17 :: else -> // r->lock == 0
18 break
19 od;
20 progress:
21 assert(r_lock == 0) // should still be true
22 r_lock = 1 // consumed resource
23 lk = 0 // freelock(&lk)
24 goto sleep
25 }
26
27 active proctype server() // interrupt routine
28 {
29 wakeup: // wakeup routine
30 r_lock = 0 // r->lock = 0
31 (lk == 0) // waitlock(&lk)
32 if
33 :: r_want -> // someone is sleeping
34 atomic { // spinlock on sleep queue
35 (sleep_q == 0) -> sleep_q = 1
36 }
37 r_want = 0
38 #ifdef PROPOSED_FIX
39 (lk == 0) // waitlock(&lk)
40 #endif
41 if
42 :: (State == Wakeme) ->
43 State = Running
44 :: else ->
45 fi;
46 sleep_q = 0
47 :: else ->
48 fi
49 goto wakeup
50 }
$ spin -run -l -f ex_5.pmlWhich, if an error is reported, can be followed with the replay command:
$ spin -p -replay ex_5.pmlThe first command directs spin to perform the verification with a search for non-progress loops (-l), while restricting to fair loops (-f).
Without going into too much detail, the counter-example that we would find if we omit the -f option could be classified as "unrealistic", because it ignores normal process scheduling rules that allow processes that are not blocked to eventually execute. This is reasonable finite progress criterion for non-blocked processes. By default though, the model checker will report all possible counter-examples, and not just the reasonable ones: it takes a demonic approach to finding errors. (Plus, just like in real life, restricting to reasonable behavior is usually somewhat more complex than not doing so...)
6. Verifying A Go-Back-N Sliding Window Protocol
This go-back-n sliding window protocol follows the description from Tanenbaum in 1989. The model below includes some annotations, with printf statements, to facilitate the interpretation of simulation trails.
1 #define MaxSeq 3 // file: ex_6.pml
2 #define inc(x) x = (x+1)%(MaxSeq+1)
3
4 mtype = { red, white, blue } // for Wolper's test
5
6 bool sent_r, sent_b // initialized to false
7 bool received_r, received_b // initialized to false
8
9 chan q[2] = [MaxSeq] of { mtype, byte, byte }
10 chan source = [0] of { mtype }
11
12 active [2] proctype p5()
13 { byte NextFrame, AckExp, FrameExp, r, s, nbuf, i
14 byte frames[MaxSeq+1]
15 chan inp, out
16 mtype ball
17
18 inp = q[_pid]
19 out = q[1-_pid]
20
21 do
22 :: nbuf < MaxSeq ->
23 nbuf++
24 if
25 :: _pid%2 -> source?ball
26 :: else
27 fi
28 frames[NextFrame] = ball
29 out!ball, NextFrame, (FrameExp + MaxSeq) % (MaxSeq + 1)
30 printf("MSC: nbuf: %d\n", nbuf)
31 inc(NextFrame)
32 :: inp?ball,r,s ->
33 if
34 :: r == FrameExp ->
35 printf("MSC: accept %e %d\n", ball, r)
36 if
37 :: !(_pid%2) && ball == red -> received_r = true
38 :: !(_pid%2) && ball == blue -> received_b = true
39 :: else
40 fi
41 inc(FrameExp)
42 :: else ->
43 printf("MSC: reject\n")
44 fi
45 do
46 :: ((AckExp <= s) && (s < NextFrame)) ||
47 ((AckExp <= s) && (NextFrame < AckExp)) ||
48 ((s < NextFrame) && (NextFrame < AckExp)) ->
49 nbuf--
50 printf("MSC: nbuf: %d\n", nbuf)
51 inc(AckExp)
52 :: else ->
53 printf("MSC: %d %d %d\n", AckExp, s, NextFrame)
54 break
55 od
56 :: timeout ->
57 NextFrame = AckExp
58 printf("MSC: timeout\n")
59 i = 1
60 do
61 :: i <= nbuf ->
62 if
63 :: _pid%2 -> ball = frames[NextFrame]
64 :: else
65 fi
66 out!ball, NextFrame, (FrameExp + MaxSeq) % (MaxSeq + 1)
67 inc(NextFrame)
68 i++
69 :: else ->
70 break
71 od
72 od
73 }
74
75 active proctype Source()
76 {
77 do
78 :: source!white
79 :: source!red ->
80 sent_r = true
81 break
82 od
83 do
84 :: source!white
85 :: source!blue ->
86 sent_b = true
87 break
88 od
89 end: do
90 :: source!white
91 od
92 }
93
94 ltl p1 { (<> sent_r -> <> (received_r && !received_b)) }
$ spin -u200 ex_6.pmlNotice that in this case, because of the printf statements in the model, we don't really need to add the -p to the simulator. The two processes named p5 are printing messages to indicate key steps in their execution. To verify the model for safety properties (assertion violations or reachable invalid end-states) we can say:
$ spin -run ex_6.pmlThe verifier will then warn us about a problem:
error: max search depth too smallThe error notice says that the default search depth was not sufficient to perform a full search. To fix that we have to use a larger depth limit than the default (10,000 steps).
There's also another change we may want to make at this step, e.g., to temporarily ignore the LTL claim in a first check. We can do so by using the compilation directive -noclaim. This leads to the following command line:
$ spin -run -O2 -noclaim -m100000 ex_6.pmlThis gives us a first impression of the complexity of the search, which is still quite manageable, but requires a fair amount of memory.
The LTL property p1 that we specified at the end of the file can be used to prove that every execution sequence where a red message is sent eventually contains a state where a red message is received, and in that state no blue message could have been received yet. This establishes that the blue message cannot overtake the red message, and the red message cannot be lost.
$ spin -run -O2 -m100000 ex_6.pml # leave the LTL property enabledNotice that the search completes faster than before, requiring a smaller statespace to be explored, because we limited the verification to the specific problem of finding a counter-example to the LTL property. For that, not all possible behaviors are relevant. (I.e., we are exploring the intersection of program behavior and property behavior only.)
References
- Bartlett, K.A., Scantlebury, R.A., and Wilkinson, P.T. `A note on reliable full-duplex transmission over half-duplex lines,' Comm. of the ACM, 1969, Vol. 12, No. 5, 260-265, Figure 3c.
- E.W. Dijkstra, `Solution to a problem in concurrent programming control,' Comm. of the ACM, 1965, Vol 8, No. 9, p. 569.
- M. Raynal, Algorithms for Mutual Exclusion, MIT Press, Cambridge, Mass., 1986, 107 pgs. (The 1986 edition is a translation from the original French version published in 1984.)
- L. Lamport, `The mutual exclusion problem -- parts I and II,' Journal of the ACM, Vol. 33, No. 2, April 1986, pp. 313-347.
- G.L. Peterson, `Myths about the mutual exclusion problem,' Inf. Proc. Letters, 1981, Vol. 12, No. 3, pp. 115-116.
- G. Berthelot, and R. Terrat, `Petri Net Theory for the correctness of protocols,' IEEE Trans. on Comm., Vol COM-30, No. 12, Dec. 1982, pp. 2497-2505.
- L.M. Ruane, `Process synchronization in the UTS kernel,' Computing Systems, (Usenix, Summer 1990), Vol. 3, No. 3, pp. 387--421.
- D. Dolev, M. Klawe, and M. Rodeh, `An O(n log n) unidirectional distributed algorithm for extrema finding in a circle,' Journal of Algorithms, Vol 3. (1982), pp. 245-260.
- M. Raynal, Distributed algorithms and protocols, John Wiley and Sons, New York, 1992.
- A. Tanenbaum, Computer Networks, 2nd Ed., Prentice Hall, Englewood Cliffs, NJ., 1989, p. 214, 232-233.
- P. Wolper, ``Specifying interesting properties of programs in propositional temporal logic,'' Proc. 13th ACM Symposium on Principles of Programming Languages, St. Petersburg Beach, Fla., January 1986, pp. 148-193.
|
Spin Online References ProMeLa Manual Pages ProMeLa Grammar Rules Spin HomePage |
(Page Updated: 15 January 2018) |